Bounded control inputs

Although constraints on the states can often be "softened", e.g., into probabilistic constraints, hard constraints on control inputs are omnipresent. This feature should be taken into account at the control synthesis stage, which leads to nontrivial difficulties in controller synthesis techniques due to inevitable nonlinearities involved.

The objective is to provide a tractable, convex, and globally feasible solution to the finite-horizon stochastic linear quadratic (LQ) problem for with possibly unbounded additive noise and hard constraints on the control policy. Within this framework one has two immediate directions to pursue in terms of controller design, namely, a posteriori bounding the standard LQG controller, or employing certainty-equivalent MPC controller. While the former direction explicitly incorporates some aspects of feedback, the synthesis of the latter involves control constraints and implicitly incorporates the notion of feedback.

Our choice of feedback policies (reported in [external page HCL09] and [external page CHL09]) explores the middle ground between these two choices: we explicitly incorporate both the control bounds and feedback at the design phase. More specifically, we adopt a policy that is affine in certain bounded functions of the past noise inputs. The optimal control problem is lifted onto general vector spaces of candidate control functions from which the controller can be selected algorithmically by solving a convex optimization problem. Our novel approach does not require artificially relaxing the hard constraints on the control input to soft probabilistic ones (to ensure large feasible sets), and still provides a globally feasible solution to the problem. Minimal assumptions of the noise sequence being i.i.d and having finite second moment are imposed. The effect of the noise appears in the convex optimization problem as certain fixed cross-covariance matrices, which may be computed offline and stored.

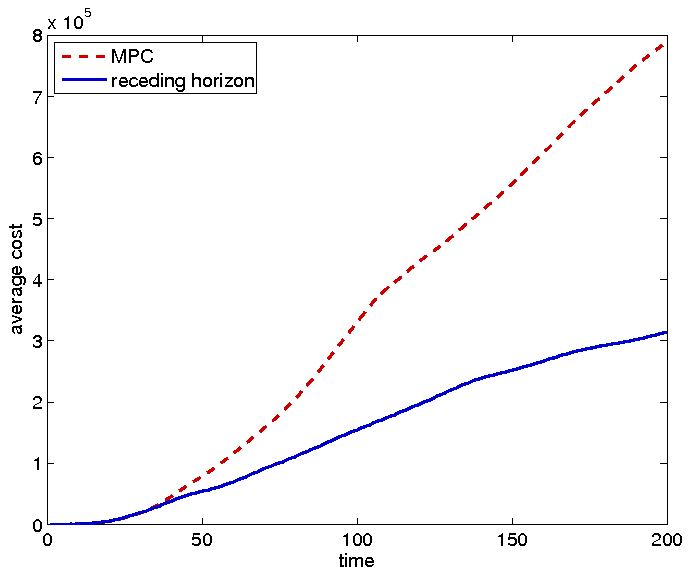
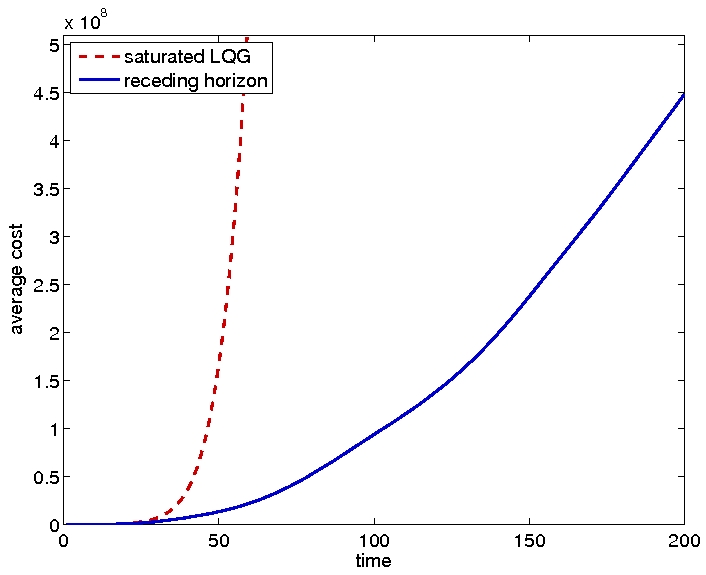
Once tractability of the optimization problem is ensured, we employ the resulting control policy in a receding horizon fashion. The above scheme requires complete observation of the state. We have also addressed the case of partial state observation in the context of linear controlled systems with i.i.d Gaussian noise; this case admits the employment of a Kalman-like filter, and may be used constructively for MPC. Performance comparisons of our receding horizon policy against certainty-equivalent MPC and saturated LQG for benchmark systems are depicted in Fig. 2 & 3.­