Bio systems
This research project is not currently active and this page is not regularly updated. It is provided here for archival purposes.

Biochemical reaction networks can be understood and controlled with the help of stochastic models. These models have to be identified from measurements of the abundance of chemical compounds inside single cells. For a successful identification it is usually critical to perturb the system in order to induce dynamic changes in the molecule abundances. These perturbations can be planned such that they optimally excite the system and lead to maximally informative data.
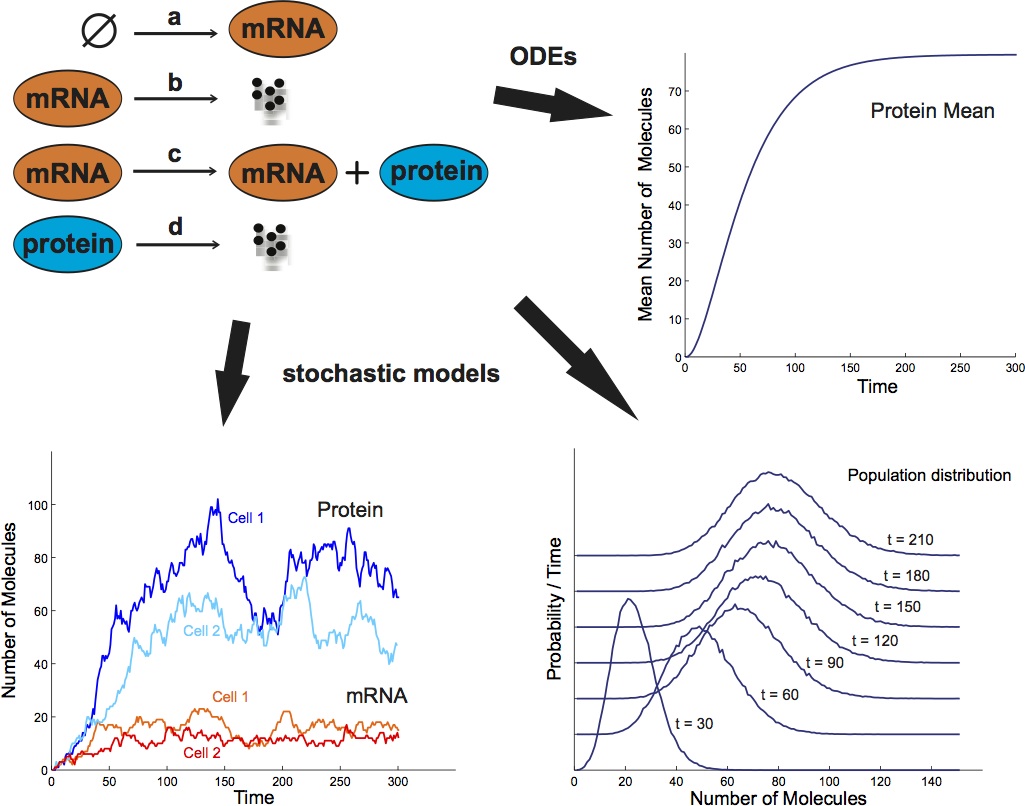
Mathematical modeling of biochemical networks has attracted considerable attention in recent years and is recognized as one of the major challenges facing the biology research community today. Most of the models available in the literature can be classified into two families: models with deterministic dynamics (e.g. ordinary differential equation models for the time evolution of the average amount of molecules in a cell population) and models with stochastic dynamics (e.g. continuous-time Markov chains which capture the dynamics of the amount of molecules in individual cells). Even though it is widely recognized that many biochemical processes involve inherent randomness, there have been very few attempts to construct such stochastic models from data. The objective of the group is, on the one hand, to develop new methods for the identification of such models from single-cell measurements and, on the other hand, to use stochastic modeling to learn about and to control real biological system.
One of the defining changes in molecular biology over the last decade has been the massive scaling up of its experimental techniques. The sequencing of the entire genome of organisms, the determination of the expression level of genes in a cell by means of DNA micro-arrays or flow cytometry and the identification of proteins and their interactions by high-throughput proteomic methods have produced enormous amounts of data on different aspects of the development and functioning of cells. A consensus is now emerging among biologists that to exploit this data to its full potential one needs to complement experimental results with formal models of biochemical networks. Mathematical models that describe gene and protein interactions in a precise and unambiguous manner can play an instrumental role in shaping the future of biology. For example, mathematical models allow computer-based simulation and analysis of biochemical networks. Such in silico experiments can be used for massive and rapid verification or falsification of biological hypotheses, replacing in certain cases costly and time-consuming in vitro or in vivo experiments. Moreover, in silico, in vitro and in vivo experiments can be used together in a feedback arrangement: mathematical model predictions can assist in the design of in vitro and in vivo experiments, the results of which can in turn be used to improve the fidelity of the mathematical models.
The following scheme illustrates the 4 main tasks involved in the analysis and control of biological systems. Our group is actively doing research in all these fields.
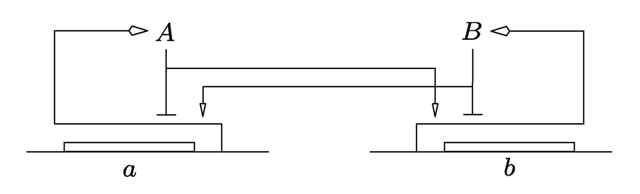
Chemical reaction networks consist of a set of distinct chemical species and a set of reactions by which the amounts of molecules that are present in the system are changed. Traditionally, such systems have mostly been modeled deterministically using the so-called reaction rate equations. These are ordinary differential equations which describe the time evolution of the concentrations of the chemical species, under the assumption of large amounts of molecules. Inside cells, however, the reaction volumes are very small and some species may be present in low abundances. Under these conditions, stochastic models proved to be necessary to explain phenomena that are not captured by deterministic models. A famous example is the bistable switch network shown in Figure 1. Therein, the switching between the two different stable equilibria of the deterministic model can be explained only using a stochastic model.
Under the assumption that the system is well-stirred, in thermal equilibrium and that the reaction volume is constant it can be shown that the amount of molecules that are present in the biochemical system follows a continuous-time Markov chain (CTMC) whose dimension is equal to the number of different chemical species. The time evolution of the probability distribution of this stochastic process follows an equation known as the chemical master equation (CME).
A question that has been much discussed lately is how much of the variability observed in biological measurements can really be attributed to random molecular fluctuations and how much stems from other factors such as differences between cells which are already present at the start of an experiment or different local micro-environments in the population. These different sources of variability are usually termed intrinsic and extrinsic noise as referring to the randomness that is intrinsically present in the biochemical process of interest and the variability that stems from factors which are extrinsic to the studied process, respectively. Biological experiments targeted to separate intrinsic and extrinsic noise have shown that both sources of variability can play an important role. Often, extrinsic noise dominates but, as dictated by theory, if the molecule counts are small, intrinsic noise becomes more important. Continuous time Markov chains and the chemical master equation offer a framework for modeling the intrinsic noise of biochemical processes. Our group works on constructing and analyzing extensions of CTMC models which also include extrinsic noise sources, mainly in the form of reaction rates that are assumed to vary randomly between different cells of the population. The major difficulty in the analysis of such models is that it is in most cases not possible to compute the time evolution of the whole probability distribution of the corresponding stochastic process.
Application: DNA replication control in the fission yeast cell cycle [1]
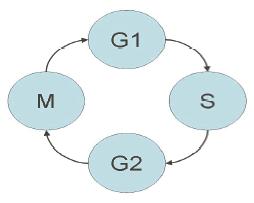
DNA replication, the process of duplication of the cell's genetic material, is central to the life of every living cell, and is always carried out prior to cell division to ensure that the cell's genetic information is maintained. Replication takes place during a specific stage in the life cycle of a cell (the cell cycle). The cell cycle can be subdivided in four phases: G1, a growth phase in which the cell increases its mass; S (synthesis), when DNA replication takes place; G2, a second growth phase, and finally M phase (mitosis), during which the cell divides into two daughter cells.
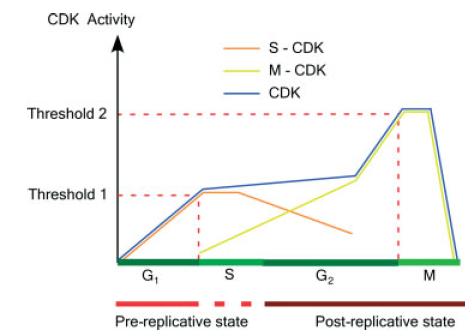
Cell cycle events are regulated by the periodic fluctuations in the activity of protein complexes called CDKs (Cyclin Dependent Kinases). There are two identified thresholds in CDK activity, see Figure 3. Threshold 1 defines entry into S phase and threshold 2 defines entry into mitosis. Complex models have already been developed for the biochemical network regulating the fluctuation of CDK activity during the cell cycle.
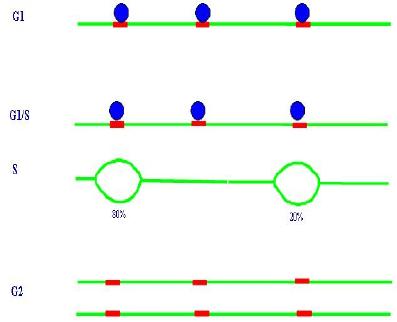
During S-phase, every base of the genome must be replicated once and only once, so that genetic information is preserved: daughter cells must have the same genetic information as their progenitor. Because genomes of eukaryotic cells are large in size and the speed of replication is limited, DNA replication initiates from multiple points along the genome, called origins of replication. Following initiation from a given origin, replication continues bidirectionally along the genome, giving rise to two replication forks moving in opposite directions, see Figure 4.
Initial models, influenced by the replication of bacterial genomes, postulated that defined regions in the genome would act as origins of replication in every cell cycle. Indeed, initial work from the budding yeast (Saccharomyces cerevisiae) identified specific sequences which acted as origins of replication with high efficiency. This simple deterministic model of origin selection however is reappraised following more recent findings which show that, especially in higher eukaryotes, a large number of potential origins exist, and active origins are stochastically selected during each S phase.
Schizosaccharomyces pombe (S. pombe, fission yeast) is a very attractive model organism for the study of the cell cycle because it is a simple unicellular eukaryote amenable to genetic and biochemical analysis. It has conserved many genes affecting cell cycle control that are typically found in higher organisms and its origin selection appears more similar to higher eukaryotes. Furthermore, and because it is very distantly related to budding yeast, the study of fission yeast can serve as a very promising complementary model system to compare global data sets of these two widely manipulated eukaryotes. In S. pombe (as well as in mammalian cells) no specific consensus sequences have been characterized that can function as an origin. Many potential origins have been mapped, but their pattern of firing shows an astonishing heterogeneity among cells in the population. This stochastic feature appears to be totally independent of successive replication events; there is no epigenetic regulation causing an origin that has fired in a cell cycle to preferentially fire or not in the next. The firing origins are not the same for every cell so, out of the pool of all possible origins, a semi-random sample will be active in a specific replication event.
Our groups has been developing stochastic hybrid models to capture the DNA replication in S. Pombe. Based on these models we have been able to draw interesting and sometimes surprising conclusions about the regulation mechanisms controling this complex process.
Quantitative studies of biological systems with mathematical models strongly depend on an appropriate characterization of the underlying system, that is on good knowledge about the underlying mechanisms and kinetic parameters. While extracting such knowledge from averaged cell population data is common practice, it has only recently been realized that also the molecular noise observed in single cell measurements may be a rich source of information about the model parameters. Mathematically, one way to quantify the information provided by single cell experiments is to determine the precision to which the model parameters can at best be estimated in a given experimental setup, that is to determine the variances of the best possible unbiased estimators of the model parameters. Thanks to the Cramer-Rao inequality these variances can be computed from the Fisher information matrix (FIM). Unfortunately, computing the FIM, to decide whether a single cell experiment might be beneficial, requires the solution of the CME and is usually very difficult for CTMC models. Our group is working on methods that aim at approximately computing the FIM. One specific mathematical trick that we use is to transition from a full description of the stochastic process to a computationally more tractable framework in which only low-order moments of the process are captured. These moments can then be used to compute the FIM for statistics of the measured single cell data and, hence, to determine lower bounds on the total information provided by the experiment. See for example [2],[3],[4] and [5].
As stated before, the FIM can be used to decide whether or not a single cell experiment should be performed. Possibly even more important, however, is that it can generally be used to compare different experiments and, hence, to search for the most informative one. This task, known as optimal experimental design, requires solving an optimization problem in which a functional (usually the determinant) of the FIM is maximized over the set of possible experiments. Our group is developing algorithms that can be used to perform optimal experimental design in realistic experimental settings and, together with our collaborators, we are also applying our methods in the wet lab. See for example [6].
The use of mathematical models is of paramount importance for the quantitative characterization of biological systems. In order to obtain such models, one typically derives the equations describing the dynamics of the compounds, starting from the available physical knowledge. These equations, however, depend on parameters that are usually unknown. A key step in the construction of a quantitative model is therefore the collection of data, from real experiments, from which the unknown parameters can be inferred. The inference process is called grey-box identification, to stress the fact that the structure of the model is known, contrary to black-box modeling where no information is available, but some pieces are missing (i.e. the parameters value). In the literature there are two main approaches for parameter identification.
- FREQUENTIST APPROACH: following this approach, a point estimate of the model parameters is computed by minimizing the distance, according to an appropriate norm, between the measured data and the model output. The Prediction Error Methods (PEM) are among the most used approaches in this context. If additional structure on the model is available, more tailored methods can be used, as done in [7] for linear systems.
- BAYESIAN APPROACH: contrary to the previous case, Bayesian inference methods return a probability distribution for the parameters. At the very core, this approach is built on the idea that prior information about the model parameters should be incorporated in the inference process. This is done by defining the parameters as a random variable distributed according to a "prior probability distribution" that should incorporate all the available knowledge. If no other information apart from the physiological range is available, then a uniform distribution can be used. After collecting the data, this "a priori distribution" is updated into an "a posteriori distribution", according to Bayes rule. Computing the posterior distribution in closed form is usually not possible, however a good approximation can be obtained from samples taken using Markov Chain Monte Carlo (MCMC) approaches.
Application: Stochastic stress responses in yeast [8]
Stress responses are among the most studied systems in yeast, yet many details about the precise functioning of the molecular mechanisms often remain unknown. One particular system that has received much attention lately is the response of yeast cells to salt stress. Salt creates osmotic pressure and the cells counter this stress by activating the Hog1 signaling cascade. The role of the kinase Hog1 is two-fold. In the cytoplasm, Hog1 phosphorylates its substrate to increase the internal concentration of glycerol in the cell. In parallel, a large fraction of the active Hog1 translocates to the nucleus where it triggers the activation of a transcriptional program leading to the upregulation of roughly 300 genes. Once the internal glycerol concentration allows to balance the external osmotic pressure, the Hog1 pathway is deactivated leading to loss of active Hog1 and a rapid termination of the transcriptional process.
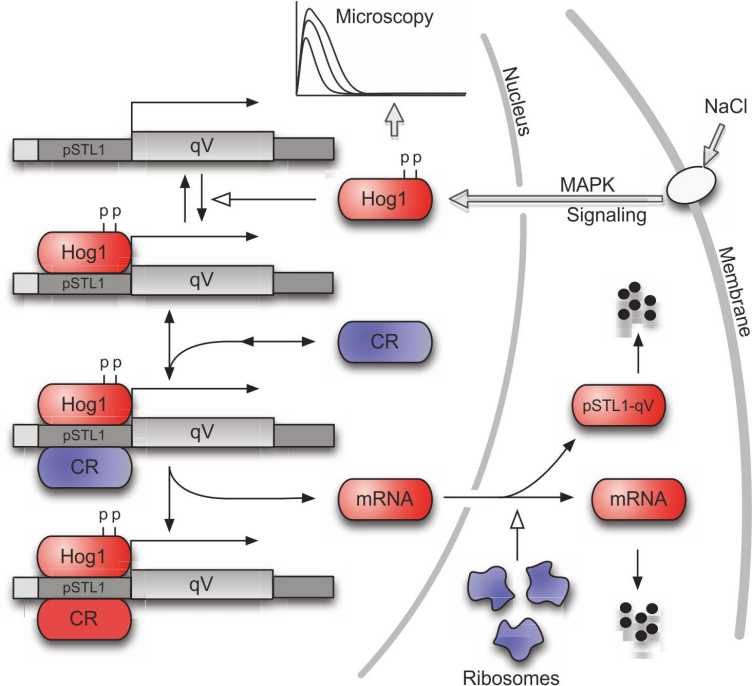
Recently, it was observed that the transient activation of the Hog1 signaling cascade results in bimodality in the profiles of the fluorescent expression reporter pSTL1-qV. In other words, for some stress conditions, even though all cells were genetically identical, only a fraction of the population used the expression of this gene as part of their stress response. This raised the question of whether there is some kind of stochastic mechanism at work which makes the cells respond differently to the same stress.
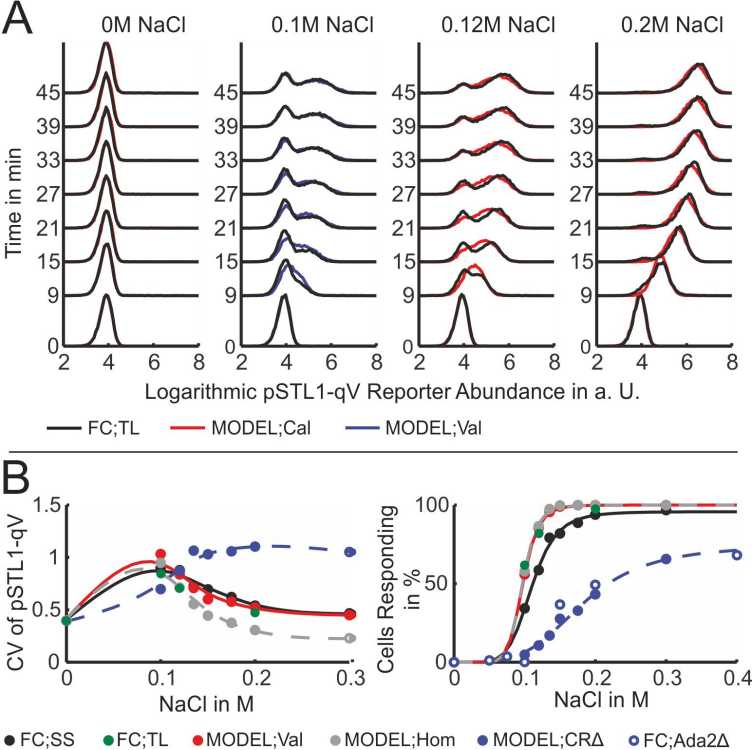
Based on flow cytometry measurements of the response of the cell population to different stress levels, our group has developed a continuous-time Markov chain model which can be used to study the role of stochasticity in this system (Figure 6). The model predicts that the percentage of responding cells as a function of the stress level is the same for homogeneous and heterogeneous populations (Figure 7) and, hence, that the observed partitioning of the cell population into expressing and non-expressing cells can be attributed to stochastic reaction events that happen in the short time when Hog1 is present in the nucleus.
Once a quantitative model of the biological system has been derived, it can be used for several different tasks.
- PREDICTIONS: the most straightforward application is the prediction of the system behavior, under different conditions or different stimuli. In particular, in the Bayesian approach, it is possible to propagate the information gained from the parameter posterior distribution into the so-called predictive distribution. This allows one to quantify how much of the parameter uncertainty is actually important to determine the behavior of the system.
- ANALYSIS: a quantitative model can also be useful to gain additional insight into the biology of the system. For example, the identified parameters can give information about the rate of the reactions (i.e. which reactions are more frequent/important). Another possibility is to use the model to study what would be the effect of removing some of the reactions (knock-out) or the effect of external stimuli.
- CONTROL: A quite interesting aspect of systems biology is that it is nowadays possible to construct biological components that react to external inputs, such as light or concentration signals. Quantitative models of such components can be used to design which signals should be applied to the system in order to obtain a desired behavior. For example, in the case study detailed below, a light signal is used to control the protein production of a gene expression circuit in yeast. In this context, a fundamental contribution can be gained from techniques developed in control theory. Viceversa, the analysis of controlled biological systems can open new theoretical challenges for control theorists. In our group, we are actively doing research on reachability for biological systems. For the system described in [9], this task turned out to be strictly related to the reachability analysis of switched linear positive systems.

