Demand response methods

The last years have witnessed a new opportunity for consumers to play a significant role in the operation of the electric grid. This is due to several factors; the recent technological improvements in home automation allow users to control the energy consumption of their houses online. Moreover, the large-scale introduction of intermittent energy sources - such as wind and solar power - causes fluctuations to the supply of energy and consequently to the price of energy. With the advanced technologies, portions of demand can shape their consumption in order to help balance the supply and demand of energy, in the face of stochastic generation, while optimizing their costs.  

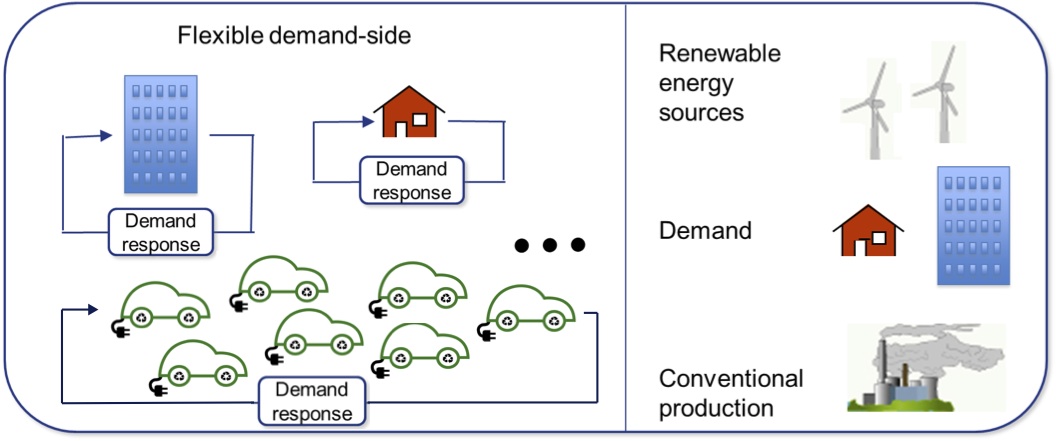
The research on demand response studies schemes in which the consumers play such important role in the operation of the electric grid. In the following we describe some possible implementations and variants.

Electric system planners and operators can use demand response programs as resource options for balancing supply and demand; in order to do this, time-based rates or other forms of financial incentives are used to steer the consumers' behaviors towards a reduction or shift of their electricity usage during peak periods. More centralized and direct schemes include direct load control programs, which give the power to energy companies of cycling air conditioners and water heaters on and off during periods of peak demand in exchange for a financial incentive and lower electric bills.

Each single consumer can receive predictions of the energy price for the following hours or days; the consumer can then exploit these predictions and plan his energy consumption for the following hours or days according to the foreseen energy prices, in order to minimize his energy bill. In this scenario one needs to account for the fact that if a large number of users adopt such ahead planning, their aggregate behavior can have a significant influence on the actual energy price.
There exists the possibility that some users aggregate and plan their behavior together in order to optimize their performance or provide power system services, such as ancillary services. In particular, an aggregator can represent the interests of the group of users; after taking agreements with them, it has the possibility of bidding into the energy market, selling or buying extra energy for its users in critical moments.  

Mean field games

In certain applications, such as system composed by a large number of thermostatically controlled loads or of plug-in electric vehicles, a completely centralized control scheme cannot be used to achieve the goals of stability, efficiency and robustness; this is mainly because in general the number of systems under consideration is too high for centralized computations and decisions; in addition to that, the users may not be willing to provide information about their daily habits to a central coordinator unit, for privacy reasons. One approach to overcome these difficulties is to allow the central coordinator (for example, the distribution system operator in power grids scenarios) to keep track of an anonymous state for the whole population of systems (for instance, in form of a probability distribution) and to steer this state by providing macroscopic incentives, such as pricing, penalties, bulk commands.
A modeling framework that inherently satisfies these requirements is that of mean field control (MFC). In this framework, each system (or agent) seeks a dynamical evolution that minimizes a cost-function depending not only on its own behavior, but also on the average behavior of the overall population. The number of agents is assumed to be very large and indeed the fundamental mathematical results on MFC are derived for an infinite number of agents. Given the systems parameters and cost functions, these results describe the evolution of the state distribution, characterize which average distributions give rise to equilibrium configurations and analyze the stability of such configurations. 

LQG models:

In the Linear Quadratic Gaussian (LQG) framework we consider a set of agents whose dynamics are described by a linear state-space model; each agent seeks a control law that minimizes its cost function; the cost function expresses a trade-off between tracking the average state (average among all the other agents) and reducing the magnitude of its control input. The term LQG refers to the fact that the cost function under consideration is quadratic and the linear dynamics are subject to Gaussian noise. This situation can model, for example, the production planning of a firm, which seeks a production level that follows the one of other firms in the market, but at the same time wants to minimize the costs associated with the actions of increasing or decreasing its production level.
In general the problem of minimizing such a cost under linear dynamics is difficult to solve, because the cost function of each agent also depends on the state evolution of all the other agents. By means of operator theory and introducing some concepts of game theory, it is possible to show that under some technical assumptions on the dynamics and on the cost function, the system of agents possesses an equilibrium configuration; in words, there exists a set of control strategies (one for each agent) for which no agent has any incentive to change strategy, because given what the others are doing the current one is its own best strategy.

PDE models:

As mentioned in the introduction, while an accurate model of the dynamics of individual systems in a population may exist, aggregating these dynamics results in a computationally intractable model. Additionally, the parameters and states of the systems are not necessarily known to a central coordinator or to other systems in the population. As such, developing a scheme to control the population power consumption is challenging due to the lack of a computationally tractable global model and limited communication between the local systems and the global coordinator. Instead of keeping track of individual system dynamics, one can model aggregate population dynamics through characterizing the probability distribution function (PDF) of the states. The PDF contains sufficient information for controlling all aggregate quantities of interest such as the mean and covariance of states. For a homogenous population of stochastic systems, the PDF evolution may be derived as a Fokker Planck Partial Differential Equations (PDE). The control problem can be formulated as a centralized or decentralized optimal control problem. The solution of this problem can then be characterized by coupling the Hamilton-Jacobi-Bellman PDE and the Fokker Planck PDE. In addition, the optimal control law for an individual system can be derived as a function of the system's state and aggregate state of the population.  

In fact, the cost of the energy varies during the night, and it depends also on the charging strategies of the other PEVs; this is exactly why the individual optimization problems for each vehicle are coupled and the system under consideration becomes difficult to analyze. As described above, it is possible to show that an equilibrium configuration exists for the system, and, more interestingly, such equilibrium gives rise to a valley-filling behavior: the aggregated electric consumption of the PEVs fills the overnight gap of the non-PEV demand, in the sense that in the central period of the night the sum of the PEV and non-PEV electricity consumptions is constant.