Modeling of hybrid systems
Introduction
The systems we are considering belong to the class of discrete-time linear hybrid systems. We define our models in the discrete-time domain, and confine them to (piecewise) affine dynamics rather than allowing general nonlinear dynamics. This avoids a number of mathematical problems (like Zeno behavior) and allows us to derive models for which we can pose analysis and optimal control problems that are computationally tractable. To model such discrete-time linear hybrid systems, we adopt Mixed Logical Dynamical (MLD) models and the Piecewise Affine (PWA) framework [1]. Other representations of such systems include Linear Complementarity (LC) systems, Extended Linear Complementarity (ELC) systems and Max-Min-Plus-Scaling (MMPS) systems that are equivalent to the MLD and PWA forms under mild conditions [2].
- [1] E. Sontag, "Nonlinear regulation: The piecewise linear approach". In IEEE Trans. Automat. Contr., vol. 26, no. 2, pp. 346-358, April 1981.
- [2] W. Heemels, B. D. Schutter, and A. Bemporad, "Equivalence of hybrid dynamical models". In Automatica, vol. 37, no. 7, pp. 1085-1091, July 2001
Main research topics:
Mixed Logical Dynamical Systems
The Mixed Logical Dynamical (MLD) framework is a powerful tool for modeling discrete-time linear hybrid systems. Its main favorable feature is its ability to model logical parts of processes (on/off switches, discrete mechanisms, combinational and sequential networks) and heuristics knowledge about plant operation as integer linear inequalities. As we are dealing with systems which have both logic and dynamics, this modeling framework establishes a link between the two worlds. Moreover, the MLD framework allows for convenient modeling using the HYbrid Systems DEscription Language HYSDEL, and is well-suited for the formulation of Model Predictive Control problems for hybrid systems.
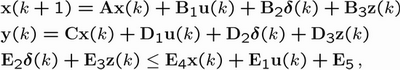
This is the general MLD form of a hybrid system where k is the discrete time-instant, and x(k) denotes the states, u(k) the inputs and y(k) the outputs, with both real and binary components. Furthermore, delta and z represent binary and auxiliary continuous variables, respectively. These variables are introduced when translating propositional logic or PWA functions into linear inequalities. All constraints on states, inputs, outputs and auxiliary variables are summarized in the mixed-integer linear inequality constraint. Note that the first two equations of the MLD model are linear; the nonlinearity is hidden in the integrality constraints on the binary variables.
We consider MLD systems that are completely well-posed, i.e. for a given pair x(k) and u(k), the values of delta(k) and z(k) are uniquely defined by the inequality. This assumption is not restrictive and is always satisfied when real plants are described in the MLD form. Note that the MLD framework allows for describing automata, propositional logic, if... then... else... statements and PWA functions. General nonlinear functions cannot be modelled and have to be approximated by PWA functions.
A. Bemporad and M. Morari, "Control of systems integrating logic, dynamics, and constraints". In Automatica, vol. 35, no. 3, pp. 407-427, March 1999.
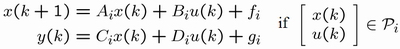
wherein u(k), x(k) and y(k) respectively represent the input, state and output of the system at time k and all matrices Ai, Bi, Ci, Di and vectors fi, gi contain real entries and are of appropriate dimension. The set Pi defines the polyhedral partition in the state-input space as shown in the figure below.
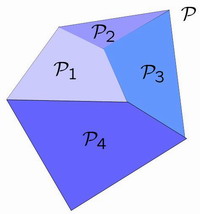
In other words, a PWA description is suitable for a system that evolves according to different dynamics depending on the specific point in the state-input space under consideration. A PWA system of the shown form is said to be well-posed if the inequality is uniquely solvable in x(k + 1) and y(k), once x(k) and u(k) are specified. PWA systems are the object of extensive research as
- they constitute an immediate extension of linear systems capable of modeling nonlinear/non-smooth phenomena with an arbitrary degree of precision and
- they allow to consider fundamental hybrid features such as linear-threshold events and mode switching.
As shown in [external page Heemels et.al. 2001], for a given well-posed MLD model there exists always an equivalent PWA representation. Equivalence implies, that for all feasible initial states and for all feasible input trajectories, both models yield the same state and output trajectories. The conversion from MLD to PWA form is performed efficiently using the mode enumeration algorithm presented in [Geyer et.al. 2003]. An introduction to PWA systems is available in [1].
[1] E. Sontag, "Nonlinear regulation: The piecewise linear approach", IEEE Trans. Automat. Contr., vol. 26, no. 2, pp. 346-358, Apr. 1981.
Inverse Optimization Models
Exploiting the fact that continuous PWA functions can be written as the difference of two continuous convex PWA functions, we have recently shown that every PWA system can equivalently be written as an optimizing process [Hempel et.al. 2015]:
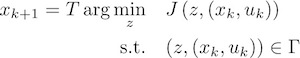
Here, uk and xk respectively represent the input and state of the system at time k. J is a (linear or quadratic) cost function, Γ is a polyhedral constraint set, and T is a linear operator. In this description, z is an auxiliary variable that solve the optimization problem defined by J and Γ and parametrized in the current state xk and control input uk. The next state is then obtained by mapping this optimal z through the linear operator T.
In [Hempel et.al. 2012] we showed that such an inverse optimization description of a PWA system is a special type of linear complementarity (LC) model. This not only extends the classical equivalence relations described in [1] but also unlocks a whole suite of computational tools to solve optimal control problems for hybrid systems. An optimal control problem for an inverse optimization model is in fact a bilevel optimization problem that can be written as an equivalent mathematical program with equilibrium constraints (MPEC), for details see [2,3].
A.B. Hempel, P.J. Goulart, and J. Lygeros, "Inverse Parametric Optimization with an Application to Hybrid System Control". Technical Report AUT14-03, June 2014 (to appear in IEEE Transactions on Automatic Control, vol. 60, no. 1, January 2015).
A.B. Hempel, P.J. Goulart, and J. Lygeros, "Inverse Parametric Quadratic Programming and an Application to Hybrid Control". In Proceedings of the conference on Nonlinear Model Predictive Control, pp. 68-73, Noordwijkerhout, NL, August 2012.
[1] W. Heemels, B. D. Schutter, and A. Bemporad, "Equivalence of hybrid dynamical models". In Automatica, vol. 37, no. 7, pp. 1085-1091, July 2001
[2] B. Colson, P. Marcotte, and G. Savard, "An overview of bilevel optimization". In Annals of Operations Research, vol. 153, no. 1, pp. 235-256, 2007
[3] Z.-Q. Luo, J.-S. Pang, D. Ralph, "Mathematical programs with equilibrium constraints". Cambridge University Press, 1996
HYSDEL
When modeling a hybrid system of any realistic degree of complexity, appropriate tools are required to efficiently and efficaciously represent and describe the model dynamics in an adequate formal setup. In particular, the MLD and PWA frameworks allow one to recast reachability/observability analysis, optimal control, and receding horizon estimation as mixed-integer linear/quadratic optimization problems; they may however embed and conceal the dynamical structure of the system in a collection of equalities and inequalities which, although computationally convenient, is cumbersome to determine manually.
In this sense HYSDEL provides a high level, intuitive textual interface for modeling a class of hybrid systems described by interconnections of linear dynamic systems, automata, if-then-else and propositional logic rules, known as Discrete Hybrid Automata (DHA). For this class of systems there exist general techniques for transforming an abstract representation into a set of constrained linear difference equations involving integer and continuous variables, and in particular the associated HYSDEL compiler translates the given description into its equivalent PWA or MLD form. The resulting MLD model can be immediately used for optimization, to solve, e.g., optimal control problems. It is also possible to generate linear complementarity (LC), extended linear complementarity (ELC) and max-min-plus-scaling (MMPS) systems, or a simulator of the model can be generated as a function in Matlab.
HYSDEL is released under the external page General Public License. The source code or the precompiled binaries are also available. MPC controllers based on HYSDEL models can be implemented with the external page Multi-Parametric Toolbox.
Mode Enumeration
Hybrid models given in HYSDEL can be considered as compositions of Discrete Hybrid Automata (DHA). In general, compositions of hybrid models are very complex, as the number of different operational modes depends exponentially on the number of component systems. The explosion of the number of possible modes leads to computational difficulties as the time and space complexity of most algorithms depends on it. Yet, most of these modes are infeasible due to the model dynamics, their interaction and additional constraints.
Using the notion of cell enumeration in hyperplane arrangements from computational geometry, we have developed an algorithm that efficiently enumerates all feasible modes of a composition of DHAs. Details can be found in [Ch. 3, Geyer 2005]. The impact of this technique is fourfold. At the modeling stage, the enumeration of modes allows the designer to understand the real complexity of the compound model. After the modeling, the model can be efficiently translated into a PWA representation, which the model is generally required to be in when deriving the PWA state-feedback control law. Compared to the related algorithm for deriving the PWA model published in [1] the one presented here is of one to two orders of magnitudes faster. During the computational stage (i.e. analysis and control), the explicit computation of the set of feasible modes of the compound system can be used as structural information to prune infeasible modes from the resulting model and thus to reduce the computational burden of related algorithms, like optimal control schemes. Furthermore, the presented algorithm is able to deal with loops that may be present in compositions, and to determine if a composition is well-posed or not.
[1] A. Bemporad, "An Efficient Technique for Translating Mixed Logical Dynamical Systems into Piecewise Affine Systems". In Proceedings of the 41st IEEE Conference on Decision and Control, December 2002.
T. Geyer, "Low Complexity Model Predictive Control in Power Electronics and Power Systems". PhD Dissertation, ETH Zürich, March 2005.
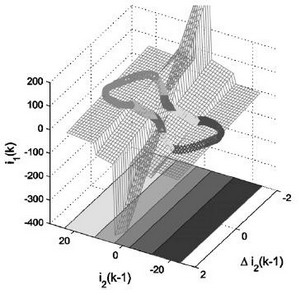
A framework for the identification of PWA hybrid systems based on the combined use of clustering, linear identification and classification techniques has been developed. The problem of identification consists of two parts. Firstly, we have to identify the polyhedral partition over which the system is defined. Secondly, the (possibly discontinuous) piecewise affine map has to be estimated. Both the affine sub-models and the polyhedral partition of the domain over which each sub model is valid is successfully identified avoiding gridding techniques. The framework needs the number of the affine sub-models as well as their order as an input.
The key idea of the algorithm lies in a procedure that reduces the problem of classifying the data to an optimal clustering problem. The main drawback of this clustering approach is the fact that it is computationally hard. A "K-means"-like algorithm that exploits confidence measures and reduces the influence of outliers and poor initializations is proposed to tackle this task. Once the data have been classified, linear regression can be used to compute the final affine sub-models. To identify the shape of the regions (polyhedral partitions) two approaches can be used. The first is based on support vector machines while the second exploits multi-category pattern recognition strategies and robust linear programming ideas.
G. Ferrari-Trecate, M. Muselli, D. Liberati, M. Morari, "A clustering technique for the identification of piecewise affine systems". In Automatica, vol. 29, no. 2, pp. 205-217, February 2003.