Theory

We work on diverse theoretical topics including new methodologies for control and identification, optimization with application to control systems (in particular stochastic and hybrid systems) and the study of complex systems:

Optimal Control at LARGE

Control theory deals with dynamical systems that can be controlled, i.e., whose evolution can be influenced by some external agent. Optimal control aims at finding a control policy for a dynamical system over a period of time such that an associated reward is maximized. Despite wide ranging progress on both the theory and applications of optimal control, considerable challenges remain when applying the existing methods to large scale systems. To address these challenges, we use optimization tools and methods to develop an approximation framework for optimal control problems: 1) energy management in buildings and districts; 2) population systems. More

Control of Constrained Hybrid Systems

Hybrid models describe systems composed of both continuous and discrete components. For hybrid systems we study novel modelling methodologies and constrained optimal controllers which are able to stabilize hybrid systems on desired reference trajectories while obeying operating constraints. In addition to fundamental theoretical advances we focus on issues of complexity and computation, facilitating application of the new methods. More

System Identification

The field of System Identification addresses the derivation of dynamic models from experimental data. The research activity at the Automatic Control Laboratory covers the application of identification techniques to physical systems as well as the theoretical development of novel identification methods. In particular, optimisation based approaches for subspace identification, where state-space models are directly obtained from time or frequency domain data, are investigated. More

Reachability

Safety and reachability are fundamental problems in systems and control. We develop the framework and algorithms to address safety and reachability of deterministic and stochastic hybrid dynamical systems, systems with multiple competing players, and systems in which the safe and target sets are dynamic and uncertain. The methods are applied to air traffic control, surveillance networks, power grid, and systems biology. More

Cooperative Control Systems

Scalable control and optimization for large-scale multi agent systems is becoming increasingly important. In the lab we approach this topic from different angles: we study non cooperative approaches formulated as mean field games, cooperative approaches based on distributed optimization and more classical approaches based on decentralized linear feedback. More

Stochastic Model Predictive Control

Robust Model Predictive Control (RMPC) is a powerful methodology to design controller for uncertain systems in which state and input constrains must be satisfied for every possible disturbance realization. In certain situations, however, this requirement may significantly degrade the overall controller performance by the need to protect against low probability outliers. Stochastic Model Predictive Control (SMPC) is a relaxation of RMPC, in which the constraints are interpreted probabilistically via chance constraints, allowing for a (small) constraint violation probability. Unfortunately, chance constrained control problems are hard in general, and must often be approximated. In our work, we focus on sampling-based approximation methods for solving such problems, and derive efficient sample sizes for both linear and non-linear SMPC problems. The methods are numerically validated on energy-efficient building control problems. More

Online Optimization as Feedback Controllers

Online Feedback Optimization is a novel way of controlling a system. The goal of such a controller is not to track a reference point, but to drive the system to an optimal point defined by an optimization problem (e.g. maximize a performance criterion). These controllers use iterative optimization algorithms and put them to use in a closed-loop control system. They can steer complex large-scale systems to an optimal point while making sure that they never leave a prescribed safe operating region. More

Data-enabled Predictive Control

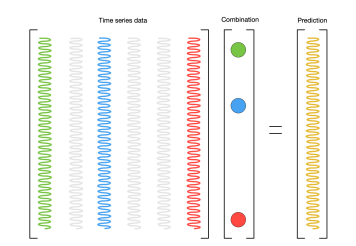
Data-enabled Predictive Control (DeePC) is a data-driven non-parametric algorithm for combined identification (learning) and control of dynamical systems. This algorithm avoids an explicit representation of the system dynamics and leverages the behavioural systems framework to implicitly describe the system trajectories using previously collected input-output data. Its receding horizon implementation is shown to be equivalent to an MPC formulation for the case of deterministic linear time-invariant (LTI) systems, while its application to nonlinear and stochastic systems is shown to be possible via different regularization techniques [1]-[3]. The cornerstones of our research are grounded in behavioral system theory, contemporary methods from statistical and machine learning, recent stochastic optimization methods, and classic control theory. More

Social Networks Dynamics

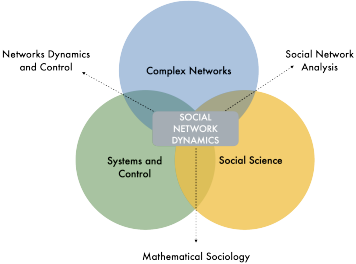
Social networks are complex systems, because of their scale, the lack of well-quantified local details, and the highly nonlinear and random dynamic interplay among individual states, interpersonal relations, global information, and multiple layers of networks. In the last decades, the rise of online social media provides enormous amount of empirical data, which makes quantitative studies of social systems possible, and in the meanwhile has also altered the pattern of how people interact. In this era of information revolution, our society faces unprecedented challenges with profound impacts on modern politics and economy, such as ideology polarization, echo chambers, and spreading of misinformation. These challenges in turn bring urgent practical significance to the study of social network systems. More