System Identification
The field of System Identification addresses the derivation of dynamic models from experimental data. The research activity at the Automatic Control Laboratory covers the application of identification techniques to physical systems as well as the theoretical development of novel identification methods. In particular, optimisation based approaches for subspace identification, where state-space models are directly obtained from time or frequency domain data, are investigated.
Identification Objectives
Obtaining systematic information from experimental observations is a key aspect of any scientific work. The obtained information leads to the formulation of a model of the system under consideration. Such a model is some form of pattern that explains the observed experimental results and allows for predictions of future system responses to be made. In our research in the field of system identification we address the problem of deriving mathematical models to describe dynamical systems. In particular, we attempt to derive tools and methods to construct dynamic models for control purposes.
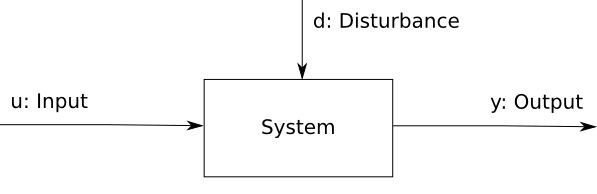
A dynamical system is an object linking observable output signals, manipulable inputs signals, and disturbances. The process of identifying a system model consists of finding mathematical functions that correlate these signals. Such a model is an approximation of the true systematic behaviour. Its complexity is a design choice and should depend on the purpose the model is designed for. Often complex models are beneficial for analysis of system behaviour. Whereas, for the design of feedback controllers simple models are generally desired.
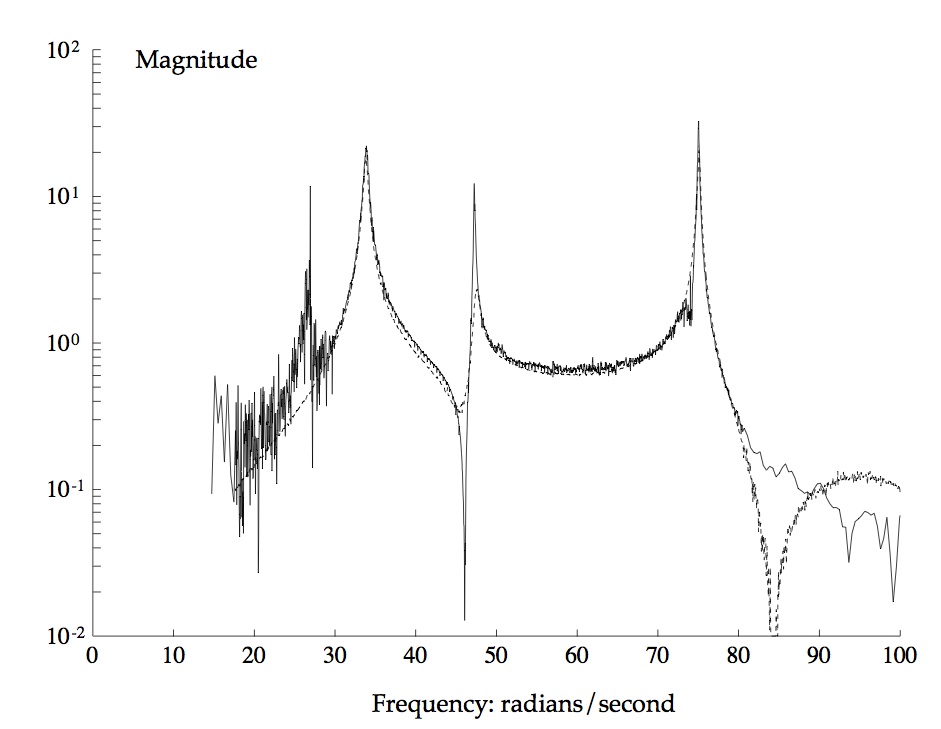
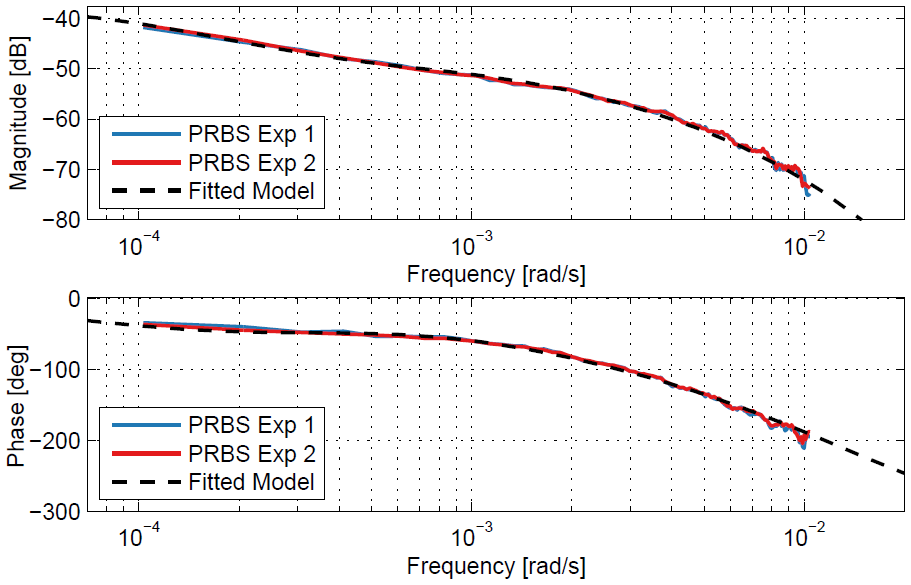
The image illustrates the fitting of a transfer function, corresponding to a linear time-invariant dynamic model of vibrations in a flexible structure, to experimental data in the frequency domain.
Identification Procedure
An identification procedure consists of designing a suitable input signal, conducting an experiment, measuring the system response, and finally using the collected data to get a model of the considered plant. The methods applied in the final identification step depend on the assumptions that are made on the model structure. In a first principles approach a parametric model derived from physical principles is built. In contrast, in a "black-box" modelling approach, the input-output relationship is estimated from experimental data only. A combination of a first principles model structure and experimental estimation of the model parameters is referred to as "grey-box" modelling.
Our research aims to investigate and extend theoretical aspects of system identification and to develop new methods and tools for practical modelling problems.
Subspace Identification
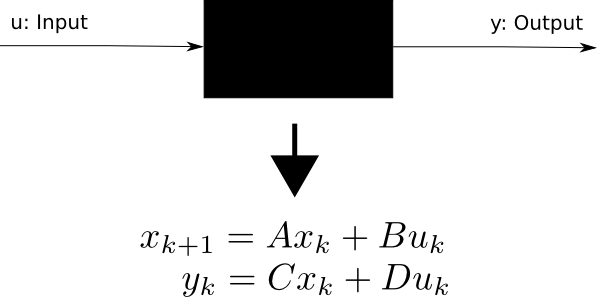
In a popular class of identification methods, known as subspace identification, linear system theory and optimisation techniques are applied to directly obtain state-space models from either time- or frequency-domain data. In this approach a linear time-invariant low order underlying system is assumed. An estimate of the observable subspace is derived from experimental data and subsequently a state-space realisation of the system is identified. This is an established approach but common implementations suffer from difficulties when the data is relatively noisy. Recently developed methods, in which the optimisation variables emulate the noise realisation corrupting the underlying system, appear to be promising in enabling the extraction of state-space models from noisy measurement data.
Nuclear Norm Minimisation
Subspace identification via singular value decomposition of rank revealing Hankel structures is an effective means of obtaining a low order model from experimental data. For the case of noisy data the singular value decomposition approach to determine the observable subspace has several problems: an incorrect weighting of the data in the singular values; difficulties in determining the appropriate rank; and a loss of the Hankel structure in the low order approximation. A nuclear norm (sum of the singular values) minimisation based method, using constraints on the noise spectrum, presents an effective technique for overcoming these problems.
The uniformly-spaced frequency domain data case assumes that the data spans the range from 0 to the Nyquist frequency:
- R. Smith, "Nuclear norm minimization methods for frequency domain subspace identification", Proc. American Control Conf., pp. 2689-2694, Montreal, Canada, 2012.
More recently, this has been extended to irregularly spaced frequency samples, and can now address the sitution where the data are generated by a frequency sweep over of limited frequency band:
- R. Smith, "Frequency Domain Subspace Identification using Nuclear Norm Minimization and Hankel Matrix Realizations", IEEE Trans. Automatic Control, Vol. 59, no. 11, pp. 1-11, Nov., 2014.
The software used to run the calculations described in this paper is publically available to those interested in experimenting with it.
- Download annihilator_method3b1.m (M, 19 KB): Generates a random system and random frequency domain samples. The subspace identification algorithm is run to produce the model order, noise size trade-off curve.
- Download annihilator_method3b1_2012_11_11c.mat (MAT, 627 KB): Data matrices for the random system used in the TAC paper.
- Download mk_figures_TAC_2012_subspace_id_v2.m (M, 9 KB): Creates the plots used in the TAC paper.
- Download blkhankel.m (M, 2 KB): Utility function to create block hankel matrices.
- Download hankel2ss.m (M, 5 KB): Utility function to create a state-space realisation from Hankel matrix data. This implements the Ho algorithm.
The code given here uses the CVX toolbox. It is not optimized. Please feel free to use this at your own risk; suitability for any purpose is not guaranteed. If you have comments I (Roy Smith) would be happy to hear them.
Solving Nuclear Norm Minimisation Problems
We have developed and implement specialised algorithms for nuclear norm minimisation problems, which arise in subspace identification. For this purpose we consider reformulations of the nuclear norm optimisation problems that are suitable for solving with convex optimisation methods, e.g. Newton method, alternating direction method of multipliers (ADMM), and dual accelerated gradient-projection (DAGP) method.
Systems Biology
We are also actively doing research on system identification theory, tailored to biological systems. In we are developing grey-box methods and Bayesian inference schemes for biochemical reaction networks.
Building Control
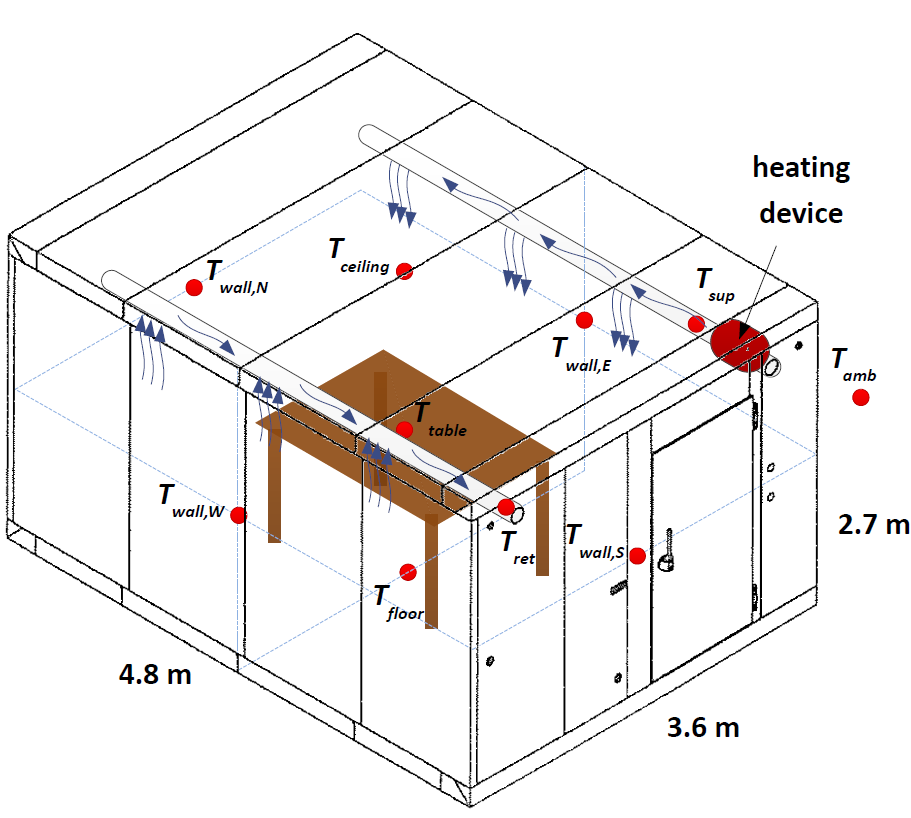
For climate control of buildings we apply system identification theory to design real world experiments and derive dynamic models of ventilated rooms.
Noise Control for Motorcycle Helmets
High acoustic noise levels in helmets are a health concern for motorcyclists. Providing good noise attenuation could lower the risk of hearing loss. Recent work on active noise control for motorcycle helmets suggests that combining feedback and predictive feed-forward control techniques can lead to promising results. Such methods involve two acoustic models, which characterise the relationship of the sound at different points in the helmet. The quality of these models is crucial for the control performance. To this end, we apply system identification methods to derive dynamic models for the helmet acoustics from experimental measurements.
Further Applications
We are applying system identification methods to a variety of other practical applications: