Cooperative Control Systems
Scalable control and optimization for large-scale multi agent systems is becoming increasingly important. In the lab we approach this topic from different angles: we study non cooperative approaches formulated as mean field games, cooperative approaches based on distributed optimization and more classical approaches based on decentralized linear feedback.
In recent years there has been an increasing need of advanced techniques for control and optimization of complex large-scale dynamical systems. Fortunately, along with the increase of complexity there have been great technological advances in the fields of communication networks and embedded computer technology. The natural approach to control such complex systems is therefore to distribute the computational burdain among different agents that, through approrpiate communication cooperatively achieve system-wide goals.
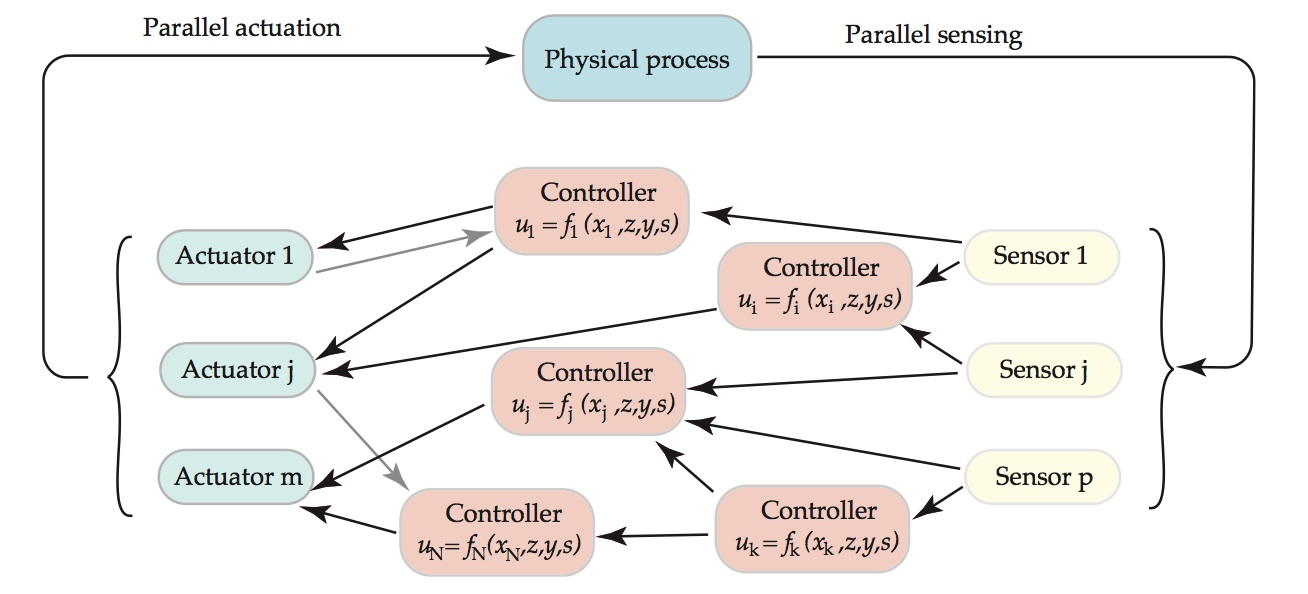
Our research focuses on the investigation of the theoretical tools necessary for decentralized control and optimization in the following fields:
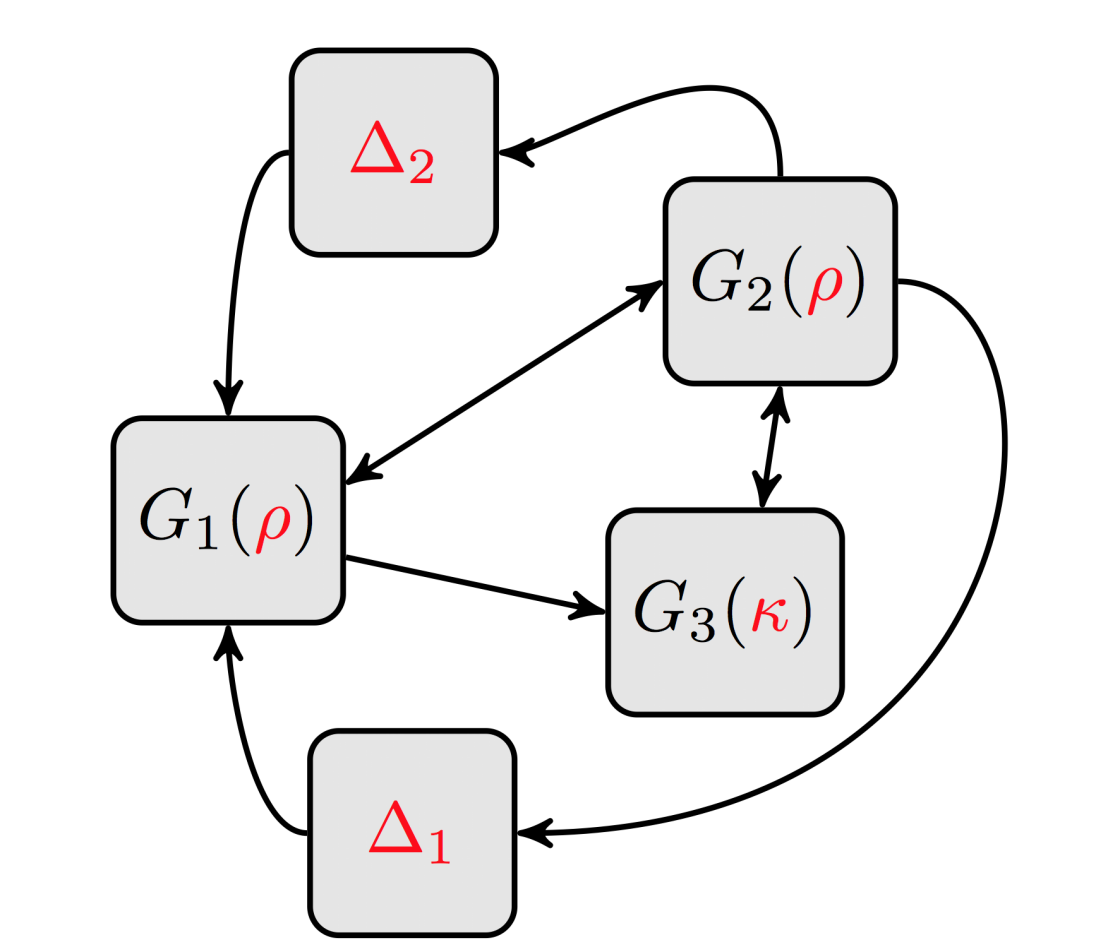
In classical linear control design decentralized and distributed control design is often equivalent to the synthesis of structured controllers. By imposing a zero-pattern to the controller one can decide which actuators have access to information form each sensor. Such stuctured control problems are hard in general. We focus on structured control design for positive systems in the presence of uncertainty and we show that for such systems the structured control problem can be solved efficiently.
A dynamical system is said to be positive if, for every nonnegative initial condition and nonnegative input, the output trajectory remains nonnegative for all time. Such systems arise naturally in several application areas including chemical reactions, population dynamics, job balancing in computer networks and consensus problems over graphs. Positive systems received increasing attention over the last decade not only for their practical relevance but also for their system theoretic properties. Recent results show that several classical hard control problems, especially those related to distributed and decentralized control, can be solved efficiently for positive systems. In [1] we show that robust stability for positive systems can be characterized as a convex feasibility problem and we use this result to design optimal distributed - decentralized controllers in the presence of uncertainty.
Cooperative Distributed Model Predictive Control
For large-scale networks of systems, which are often subject to communication constraints, feedback controllers have to be operated in a distributed way. In particular, each system in the network has to take local control decisions based on local measurements and communication with neighboring systems. A possible approach, which is suited in particular for constrained networks of systems with a common objective function, is cooperative distributed model predictive control (MPC). This control scheme has many possible applications such as power grids, traffic networks or wind farms [2]. In cooperative distributed MPC, similarly as in centralized MPC, a globally defined finite horizon optimal control problem is solved in every time step. As opposed to centralized MPC however, this problem is solved by a distributed optimization method which works under the given communication constraints, such as the alternating direction method of multipliers or dual decomposition based on fast gradient updates. Consequently, research on cooperative distributed MPC is mainly concerned with the impact of distributed optimization on system properties such as stability, feasibility, etc. Such issues arise for instance in the formulation of stable cooperative distributed MPC controllers [3], [4], [5] or in the convergence properties of distributed optimization methods when used to solve MPC problems [6].
Decentralized Mean Field Control of Large Populations of Systems
We investigate the control of large populations of dynamical systems. In this framework, each system (or agent) seeks a dynamical evolution that minimizes a cost-function depending not only on its own behavior, but also on the average behavior of the overall population. A centralized control scheme cannot be used to achieve this goal, mainly because in general the number of systems under consideration is too high for centralized computations and decisions; We use the theory of Mean Field Control (MFC) to devise decentralized control schemes that steer the population towards Nash Equilibrium. In [7] we use this scheme to control the charging of a large population of Plug-in Electric vehicles. For more information on the theorethical tools and the applications of mean field control please visit the page of the Demand Response Methods for Energy systems group.
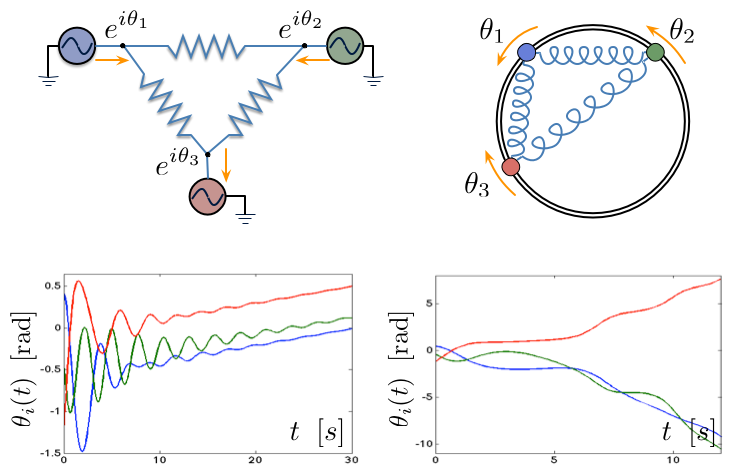
The emergence of synchronization in a network of coupled oscillators is a fascinating in various scientific disciplines ranging from neuroscience, physics, and biology to social networks and engineering. A coupled oscillator network is characterized by a population of heterogeneous oscillators and a graph describing the interaction among the oscillators. These two ingredients give rise to a rich dynamic behavior that keeps on fascinating the scientific community. An extensive survey on the theory of complex oscillator networks and their applications in power grids can be found in [8] for a tutorial. On the theory side of work, we focus on quantifying the trade-off between coupling and heterogeneity that leads to synchronization [external page 9], [external page 10]. On the application side, we are interested in how to use coupled oscillator theory for transient stability assessment in bulk power systems [external page 11], distributed control and optimization in microgrids [external page 12], [13], as well as novel computational approaches to power flow [external page 14].
Related applications:
We are motivated by applications in heterogeneous fields:
Demand response methods
Digital fabrication
Control of the Swiss free electron Laser
- Marcello Colombino and Roy S. Smith,"A Convex Characterization of Robust Stability for Positive and Positively Dominated Systems", IEEE Trans. Automatic Control, 61(7), pp. 1965-1971, 2016.
- Marcello Colombino, Andreas B. Hempel and Roy S. Smith, "Robust stability of a class of interconnected nonlinear positive systems," Proc. American Control Conf., pp. 5312-5317, 2015.