Analysis
Although stability of a linear system can be easily checked with the roots of the characteristic equation, nonlinear systems complicate matters enormously: already for a constrained linear system, stability cannot be globally proven with these methods. In general this problem is either NP-complete or undecidable. Moreover, it is also hopeless to deduce the stability/instability of a PWA system from the stability/instability of its affine subsystems.
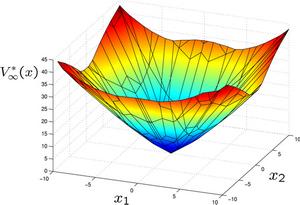
A wide range of methods with varying degrees of conservativeness have been developed for analyzing stability of PWA systems based on Lyapunov theory. Since there's no standard method to construct Lyapunov functions, algorithms for a broad class of candidate functions have been developed, e.g. computation of common quadratic, common quartic, piecewise affine, piecewise quadratic and piecewise quartic Lyapunov functions. These can be efficiently computed with linear programming, semi-definite programming and sum-of-squares techniques.
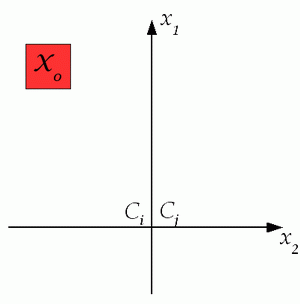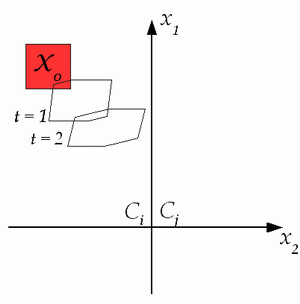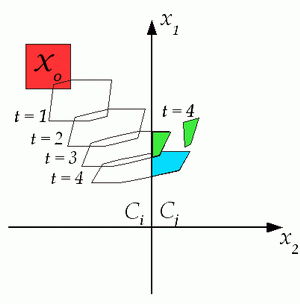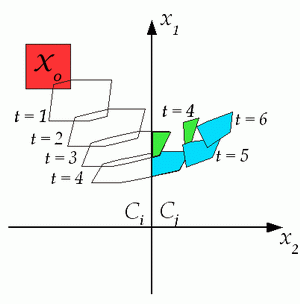
Reachability analysis (also known as safety analysis or formal verification) aims at detecting if a hybrid system will eventually reach an unsafe state configuration or satisfy a temporal logic formula. Formal verification is strictly related to the modeling framework used to describe the process, whose safety properties we need to certify. Different models lead to different verification algorithms.
For PWA and MLD systems algorithms based on mixed-integer linear programming have been developed to decide finite-time reachability. The reachability analysis relies on a reach-set computation, i.e. the computation of all reachable states starting within an initial set. The figure shows the evolution of reachable sets during a guard-line crossing of two regions Ci and Cj with different dynamics.
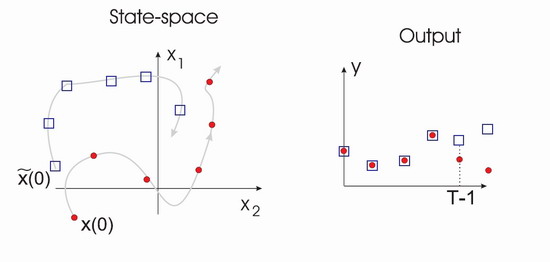
Observability is crucial for understanding if and how well a state observer for hybrid systems can be designed. Controllability in turn is an important property for the feasibility of the control design process. For piecewise affine systems observability and controllability properties cannot be easily deduced from those of the component linear subsystems. In order to analyze these properties, numerical tests based on mixed-integer linear programming have been proposed. Optimization of a PWA performance index can be used to efficiently decide controllability and observability.
Moreover, the test for controllability returns the minimum number of steps needed to steer every state of an initial set to a given target set. Respectively, with the method for observability one can determine the length of the output sequence needed to observe the system's state. The figure below shows exemplarily the evolution of the state and output for two different initial conditions that can be distinguished after 5 samples.