Randomized MPC
In general, the chance-constrained finite horizon optimal control problems that need be solved at each time step are intractable, because they are in general non-convex and require the computation of multi-dimensional integrals. Hence, SMPC is computationally infeasible for many applications. One way to obtain a tractable approximation of SMPC is by means of Randomized MPC (RMPC). The strength of RMPC is that it is not limited to specific probability distributions of the uncertainty. Indeed, the exact probability distribution need not even be known, and historical data in terms of samples suffice.
The basic idea of RMPC is to replace the chance constraints with a finite number of sampled constraints, which correspond to samples of the uncertainty distributions. From a practical point of view, these samples often arise in form of historical data. For example in building climate control, one source of uncertainty is due to the uncertainty in the weather predictions. Since typically a large amount of historical weather data is available, such data can be used to generate uncertainty samples. The main question in Randomized MPC is to determine the appropriate sample size. In general, they should be chosen as small as possible (since each sample corresponds to an additional constraint), while satisfying the chance constraints.
In the SMPC group, we mainly study two classes of systems, namely those with linear dynamics as well as control-affine systems. For both classes of systems, we derive efficient sample sizes. Our approaches to solve such problems are mainly based on the so-called scenario approach, which is a randomized technique for solving convex chance-constrained systems. For uncertain linear systems, we show that under affine feedback policies and polyhedral constraints, the required sample size grows linearly in the prediction horizon, compared to quadratically as predicted by existing bounds. The new bound has two advantages: 1. Problems that could previously not be solved due to the large amount of sampled constraints can now be solved. 2. The obtained solutions are less conservative both in terms of violation probability and consequently also in terms of cost.
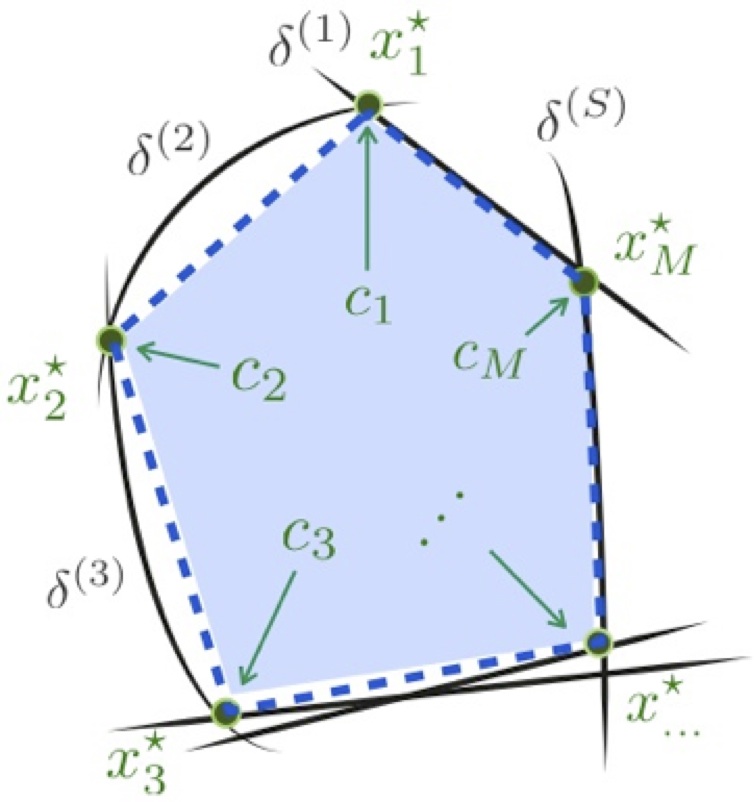
The second problem class in SMPC we study is the family of control-affine systems, which are in general non linear. This renders the sampled finite horizon optimal control problem non-convex, such that results from the standard scenario approach cannot be applied directly. Moreover, since in non-convex programming one in general has no hope to obtain the global optimum and solvers usually get stuck at local minimizers, we design a method that promises feasibility for any point inside a given set. This is illustrated in Fig. 1, where the set feasibility set is given as the convex hull of M points. We show that if the sample size is chosen quadratically in the number of inputs, then any (local) minimizer attained in the spanned polyhedron will enjoy the probabilistic constraints.