Computational issues
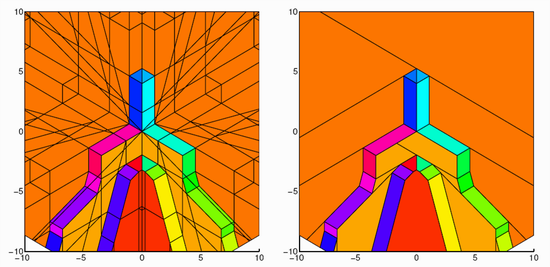
The complexity of a PWA system, which is approximately given by the number of polyhedra, is often required to be as small as possible. As an example consider the case where the state-feedback control law is computed off-line based on a PWA model. Due to the combinatorial nature of the problem, both the computation time and the controller complexity are in the worst case exponential in the number of polyhedra of the PWA model.
Hence, we have proposed two optimal complexity reduction algorithms that solve the problem of deriving a PWA model that is both equivalent to the former and minimal in the number of polyhedra. Both approaches are based on the notion of cells and markings in hyperplane arrangements. The first algorithm executes a branch and bound on the markings yielding a new set of disjoint polyhedra, where additional heuristics on the branching strategy are employed to reduce the computation time. The second approach relies on the fact that the optimal complexity reduction problem can be reformulated as a logic minimization problem by replacing the markings by Boolean variables and minterms. The resulting polyhedra are in general non-disjoint (overlapping). As both algorithms refrain from solving additional linear programs, they are not only optimal but also computationally feasible. The applicability of the algorithms can be extended to general PWA systems lacking the hyperplane arrangement (like PWA state-feedback control laws) by first computing the hyperplane arrangement. Moreover, the hyperplane arrangement can be simplified to further reduce the number of resulting polyhedra by allowing for an adjustable degree of sub-optimality. Apart from this, the notion of the hyperplane arrangement can be also used to efficiently implement PWA state-feedback control laws.
T. Geyer, "Low Complexity Model Predictive Control in Power Electronics and Power Systems", (Chapter 4). PhD Dissertation, ETH Zürich, Switzerland, March 2005.
In order to efficiently calculate explicit control laws, or to perform tasks like reachability analysis, verification, or stability analysis, it is often necessary to solve computational geometry problems. A rich library for these kind of operations has been developed and made available as part of the external page Multi-Parametric Toolbox.
The library contains routines to perform various operations on convex polytopes and non-convex unions of polytopes, such as:
- Computation of convex hulls and envelopes
- Enumeration of extreme points of polytopes
- Convexity recognition of unions of polytopes
- Set difference, Minkowski sum, Pontryagin difference operations
- Efficient computation of projections
- Intersections of polytopes
- Approximation of polytopes by ellipsoids
- Computation of minimal representations of polytopes
M. Herceg, M. Kvasnica, C. Jones, and M. Morari, "Multi-Parametric Toolbox 3.0". In Proceedings of the European Control Conference, pp. 502-510, Zürich, CH, July 2013.
Lagrangian Decomposition
Model Predictive Control (MPC) as a control scheme intrinsically and extensively relies on optimization techniques to yield the desired optimal control input. For large systems and models this typically translates into a cumbersome optimization problem for which it may not be possible to determine the exact solution with the available online computation times. For certain classes of systems however, consisting of a large number of interconnected sub-components, one classic technique to circumvent this issue is to employ Lagrangian decomposition. Specifically, for such systems relaxing relatively few interconnection constraints results in a (relaxed) decomposable problem whose optimal solution will yield, by construction, strong lower bounds to the optimum of the original problem. Determining the best lower bound possible is equivalent to solving the convex, non-differentiable dual problem whose solution may be attained by exploiting simple and relatively efficient iterative convex techniques such as the sub-gradient or the cutting planes method.
A good (suboptimal) feasible solution to the original problem, corresponding to an upper bound on the optimum, may then be constructed on the basis of the highest lower bound obtained. The resulting gap between the lower and upper bound certifies the quality of the achieved solution.
A.G. Beccuti, T. Geyer, and M. Morari, "Temporal Lagrangian Decomposition of Model Predictive Control for Hybrid Systems". In Proceedings of the IEEE Conference on Decision and Control, Atlantis, Bahamas, December 2004.